1. 背景
说起二叉树,最常见的就是对二叉树的遍历了。
针对二叉树有多种顺序的遍历方法,本文中将对这些不同顺序的遍历进行统一的梳理。
对于一个算法,明确输入输出很重要,针对遍历操作这类的问题,我们可以明确以下输入输出(本文中所有相关代码均使用Java实现):
- 输入:一个二叉树的根节点 root;
- 输出:一个包含有特定序列的List;
而二叉树的遍历,则是由非常多的遍历方式,这里我们只是找一些很常见的,同时也是在 lintcode 上有相应的题目的遍历(本文所给出的代码,均以在lintcode 上提交并且通过)。
先看一个简单的二叉树吧:
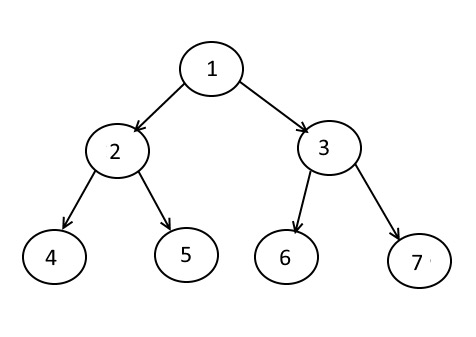
以上图的二叉树为例,有以下典型的遍历:
- 前序遍历(Preorder Traversal):1245367
- 中序遍历(Inorder Traversal):4251637
- 后序遍历(Postorder Traversal):7635421
- 层序遍历,即广度优先搜索(Levelorder Traversal):1234567
- 锯齿形遍历(Zigzag Levelorder Traversal):1324567
下面的章节将会按个介绍以上的遍历。
2. 前中后序遍历
lintcode 相关题目:
66. 二叉树的前序遍历
二叉树的前中后序遍历,基本上是最最常见的二叉树的操作,所用的方法也都是类似的,所以这里放在一起介绍。
先说下定义,所谓的前序遍历,即是把二叉树每一个结点都按照“根-左子结点-右子结点”的顺序依次遍历。前序中的这个“前”字,就是说跟结点在前。类似的,中序和后续也是指跟结点的位置在中间和在最后。
遍历是一个最常见的递归问题,因为每一个二叉树都可以看作3个部分:
- 根结点
- 左子树:一个新的二叉树
- 右子树:一个新的二叉树
前中后序的遍历问题遍历,就可以简化为对这个三个部分的遍历。以前序遍历为例,可以用以下步骤表示:
1. 声明装结果的数据result;
2. 把根结点装到 result 中;
3. 把左子树装到 result 中;
4. 把右子树装到 result 中;
5. 结束,返回resulr;
那么可以根据以上的分析很方便写出前序遍历的Java代码:
类似地,也可以很方便写出中序和后续的遍历:
3. 层序遍历(广度优先搜索)
lintcode 相关的题目:
69. 二叉树的层次遍历
70. 二叉树的层次遍历 II (该题目的解法和69的类似,本文不再赘述)
层序遍历又称为“广度优先搜索”,我个人认为“层序遍历”这个说法比较直观又形象,所以本文中都将称之为“层序遍历”。层序遍历直观上来说就是把一颗二叉树一层一层地进行遍历。
首先,我们来明确一下层序遍历算法的输入和输出,这个和之前的前中后序遍历稍微不同,层序遍历的返回输出结果是一个嵌套的数组,以下图为例:

它的层序遍历,严格来说是这样的:
即它输出的每一层的数据,都应该在一个独立的列表里面,最终再组成一个完整的结果。
我们分析下这个问题,二叉树的每一层的数据是怎么获取到的呢?很明显,每一层的数据都是上一层的所有的结点的子结点按照从左到右的顺序来排列,而上一层的数据右来自上上一层,那么最开始的来源就是根,根结点就是第一层的数据。
那么,层序遍历的步骤就是:
1. 获取第i的结点列表list;
2. 遍历list,把list中的每一个结点添加到result中;同时保存每一个结点的孩子结点到levelList 中,这个levelList就是下一层的结点列表;
3. 以levelList为下一层的数据,做第i+1层的遍历;
以上过程中,可以使用一个队列来存储临时的levelList,代码如下:
|
|
4. 锯齿形遍历
lintcode 相关题目
71. 二叉树的锯齿形层次遍历
锯齿形遍历,是在层序遍历的基础之上的一个变种,它的定义如下:
给出一棵二叉树,返回其节点值的锯齿形层次遍历(先从左往右,下一层再从右往左,层与层之间交替进行)
这个本质上还是层序遍历,只是在层序遍历的时候,需要根据当前的层数是奇数还是偶数,来做一些稍微的区分,在奇数层数据的添加顺序是从左往右,偶数层是从右往左,整体逻辑和层序遍历是一致的。
代码如下:
以上,就是关于二叉树常见的遍历啦。

