【算法题】如何判断一个单向链表是否有环？

1. 问题简介

如何判断一个单向链表是否包含有环？

这是一个关于单向链表非常经典的问题，在lintcode上也有相关的题目102. 带环链表

这样的比较小但是又足够经典的小算法，通常是在企业面试的时候会经常容易被拿出来考候选人的。接下来，我们就分析下这个问题的解体思路。

2. 问题分析

要判断一个链表是不是有环，那么我们首先得弄明白有环链表的特性是什么。然后根据有环链表的特性与无环链表的差异，来确定问题的解决方案。

有环的链表长这个样子：

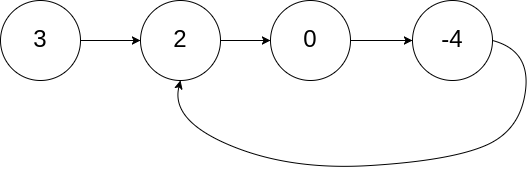
circularlinkedlist

我们可以分析一下，这样的链表有什么特性呢？

a. 它有头结点，但是没有尾结点；

b. 它的内部，包含有一个环状链表；

这个环状链表是一个有意思的链表，它是把一个链表的尾结点，指向了它的头结点。这个结构很像是柏拉图提出的“衔尾蛇“。

衔尾蛇

抛却它的哲学意味来说，但从数据结构层面来说，环状链表也是一个在特定场景中非常有用的数据结构，比如用来解决约瑟夫问题。

那么，关于环状链表，它有哪些特性呢？

a. 它无头无尾，任意结点都是平等的；

b. 若从任意结点便利它，那么遍历永远不会停止（听起来好像是废话，但是其实不是）；

关于单向链表，它的操作其实很有限，无非就是遍历、添加、移除这样的操作，但是这个环状的链接就很让人头疼，因为它遍历起来是停不下来的，所以得从其他角度考虑。

比如说，搞两个遍历同时进行，而且给两个遍历以不同的速度运行，那么根据环的特性，这两个不同速度的遍历指针，肯定会有相交的时候。

想象一下我们的田径运动的400米环形操场，在比赛开始之后，第一名的速度足够快，追上最后一名，这种第一名又一次遇到了最后一名的情形，我们俗称“套圈儿”。

没错，我们也可以把这个“套圈儿”的思路用在环状链表的遍历上，那么我们可以总结出环状链表的第三个特性：

c. 环状链表中，两个指针以不同速度遍历的话，会出现“套圈儿”的现象。

而普通的单向链表是绝对没有这样的特性的。

于是，我们就找到了一个关键的特性，用于区分普通单向链表和有环链表。

3. 解法步骤

有了上一章节的分析，我们有了一个重要的结论，即可以使用有环链表中“环”的“套圈儿”现象来区分有环链表和无环链表。那么，接下来就是解体的思路了。

我们声明两个指针，一个叫快指针”fast”，另一个叫慢指针”slow”；
接下来随便选一个节点A，从A开始遍历，fast 节点一次移动两个位置，slow一次移动一个位置；
如果fast 或者 slow中有任意一个遍历到了结尾，那么证明这个链表没有环；
如果fast 和 slow 在开始之后又一次相遇了（slow被套圈儿了），那么说明这个链表有环；

这样，这个问题就能解决了，下面给出参考代码(Java 版)。

/**
* Definition for ListNode
* public class ListNode {
*     int val;
*     ListNode next;
*     ListNode(int x) {
*         val = x;
*         next = null;
*     }
* }
*/
/**
 * @param head: The first node of linked list.
 * @return: True if it has a cycle, or false
 */
public boolean hasCycle(ListNode head) {
    // write your code here
    // 空列表无环
    if (head == null) {
        return false;
    }
    // 初始化快慢两个指针
    ListNode fast = head, slow = head;
    while (true) {
        // 快指针，步进两步
        fast = fast.next;
        if (fast == null) {
            return false;
        }
        fast = fast.next;
        // 慢指针，步进一步
        slow = slow.next;
        if (fast == null || slow == null) {
            // 无环
            return false;
        }
        // 快慢指针相遇，有环
        if (fast.val == slow.val) {
            return true;
        }
    }
}